Explanation of state-space modeling of systems for controls. Recall from the State-Space Tutorial page we can use a pole placement technique to obtain the desired output.
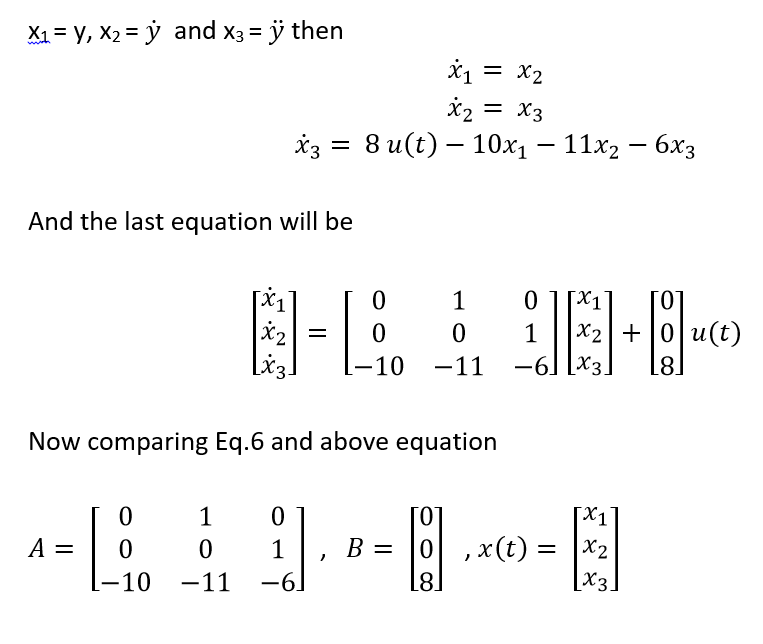
Control System State Space Model Javatpoint
Dynamical Linear Models can be regarded as a special case of the state space model.

. Linear and angular velocity command is executed. State space models 3. The dependence structure and evolution of the two time series comprising a simple univariate statespace model.
It describes a system with a set of first-order differential or difference equations using inputs outputs and state variables. A representation thof the dynamics of an N order system as a first order differential equation in an N-vector which is called the state. A Dependence relationships with arrows demonstrating that once the dependence of the observations y t on the states z t is accounted for the observations are assumed independent.
Basic system model using the State-Space block. Its many applications include. Second order mass-spring system.
At this point the model is very general and an equation of any order can be set up for solution in the block parameters. Acker lsim place plot rscale Matlab commands from the control system toolbox are highlighted in red. U r - Kx r - Kv control input.
Ft is a p m matrices. 1 2 where is an n by 1 vector representing the systems state variables is a scalar representing the input and is a scalar. Y t μ t γ t ε t t 1 T 11 where μt.
Define State-space Model A 0 1 -1 -3 B 1 0 C 1 0 D 2 ssmodel controlssA B C D H controlss2tfssmodel printH Step response for the system t y controlstep_responseH pltplott y plttitleStep Response H pltxlabelt pltylabely pltgrid pltshow 0 0 1 1 3 0 1 0 1 0 0 2 State-space Model. Multivariable and State Space MPC V20. Gt is a p p matrices.
Yt μt γt εt t 1 T. 1 The local level model. This article is a tutorial describing the process and issues related to developing a state-space model for the stochastic errors affecting an Inertial Measurement Unit IMU.
A state-space model is commonly used for representing a linear time-invariant LTI system. Convert the Nth order differential equation that governs the dy namics into N first-order differential equations Classic example. K state-feedback gain matrix.
We know the state space model of a Linear Time-Invariant LTI system is - dotXAXBU YCXDU Apply Laplace Transform on both sides of the state equation. Non-standard Matlab commands used in this tutorial are highlighted in green. Poles of a closed-loop system can be found from the characteristic equation.
If the entire state space for a problem is given then it is possible to trace the path from the initial to goal state and identify the sequence of operation required for doing it. State-space models parameterize the observed dependent variables as functions of unobserved. Where X and X are the state vector and the differential state vector respectively.
The state-space representation was introduced in the Introduction. The blue and red. Vt is a m m varianceco-variance matrix.
The state space model of Linear Time-Invariant LTI system can be represented as X A X B U. As planned this is the second part of the MPC series. Recall from my tutorial on state space modeling that the A matrix F matrix in Wikipedia notation is a 33 matrix because there are 3 states in our robotic car example that describes how the state of the system changes from time k-1 to k when no control ie.
State space model. The first and the second equations are known as state equation and output equation respectively. Advantages of State Space Search.
State-Space Modelling by Kevin Kotzé. For a SISO LTI system the state-space form is given below. MPC Tutorial II.
This lecture introduces the linear state space dynamic system. Where all the distributions are Gaussian. Lets introduce the state-space equations the model representation of choice for modern control.
In this chapter let us discuss how to obtain transfer function from the state space model. The first program for this session makes use of a local level model that is applied to the measure of the South African GDP deflator. The determinant of the sI-.
To dealing with multivariable state-space model is most convenient. 1 An Intuitive Example of a State Space Model. Once again the first thing that we do is clear all variables from the current environment and.
State space model tutorial In control engineering a state-space representation is a mathematical model of a physical system as a set of input output and state variables related by first-order State-Space Models 1 14384 Time Series Analysis Fall 2007 Professor Anna Mikusheva Paul Schrimpf scribe Novemeber 15 2007 revised November 24 2009. ARIMA and RegARMA models and dlm 5. The linear state space system is a generalization of the scalar AR1 process we studied before.
Y C X D U. ARMA models in state space form AR2 model y t 1y t 1 2y t 2 e t e t NID0 2 Let x t y t y t 1 and w t e t 0. Then y t 1 0x t x t 1 2 1 0 x t 1 w t Now in state space form We can use Kalman filter to compute likelihood and forecasts.
It is very useful in AI because of it provides a set of all possible states operations and goals. Create analyze and use state-space representations for control design. Wt yt xt NmFt xt.
This video is the first in a series on MIMO control and wil. The setup program returns a function handle for the online MPC controller. In the absence of these equations a model of a desired order or number of states can be.
Representing dynamics of higher-order linear systems. B Our toy model Eqs. Key Matlab commands used in this tutorial.
U and Y are input vector and output vector respectively. This is contained in the file T4-llmR. This model is a workhorse that carries a powerful theory of prediction.
The equation inside the State-Space block is. C0 xt xt 1 NpGt xt 1. A time series is a set of observations y1 yn y 1 y n ordered in time that may be expressed in additive form.
State-space equations Control design using pole placement Introducing the reference input Observer design. Transfer Function from State Space Model. There are several different ways to describe a system of linear differential equations.
In this part a tool to setup the state-space model based predictive controller is provided. Statas sspace makes it easy to fit a wide variety of multivariate time-series models by casting them as linear state-space models including vector autoregressive moving-average VARMA models structural time-series STS models and dynamic-factor models. U u y Cx D x Ax B 1 This represents the basic state-space equation where x a vector of the first-order state variables y the output vector x.

Intro To Control 6 1 State Space Model Basics Youtube

State Space Representations Of Linear Physical Systems

State Space 11 Tutorial And Worked Examples Youtube

State Space Representations Of Linear Physical Systems

State Space Analysis Of Control System Electrical4u

State Space Models Matlab Simulink

0 comments
Post a Comment